很高興看到大家對於選擇權有興趣,很熱衷於學習選擇權的知識。而各位如果繼續在選擇權這條路上學習,就一定會接觸到選擇權的風險係數指標,通常用希臘字母來表示,分別為Delta(δ)、Gamma(γ)、Theta(θ)、Vega(ν)、Rho(ρ),而今天我們要介紹的是在這些風險係數中佔有十分重要地位的Delta。
Delta的介紹
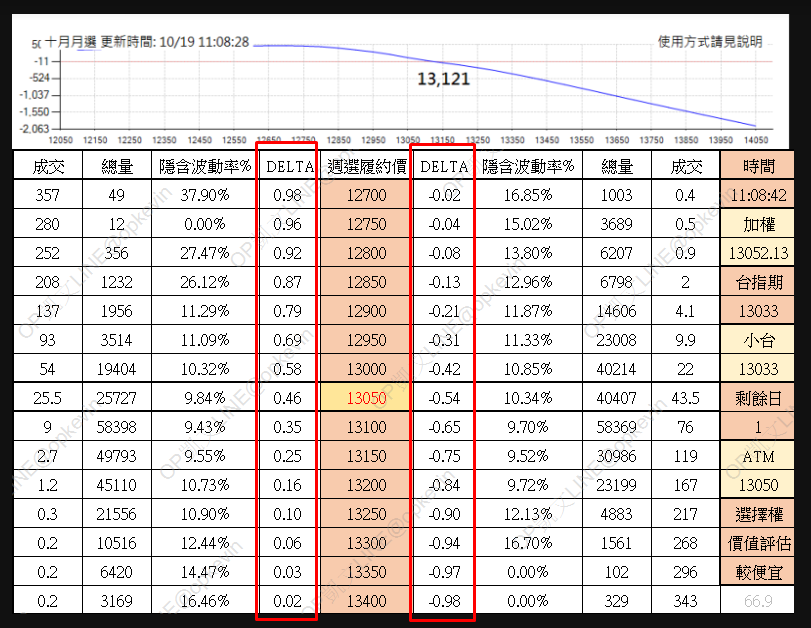
Delta是一個指標,用來告訴你當標的物的價格上漲一單位時,權利金的變動會是多少單位。舉例來說,你看到Delta 0.5,代表標的物上漲一點,選擇權權利金增加 0.5點。反之,如果你看到Delta -0.5,代表標的物上漲一點,選擇權權利金會減少 0.5點。
Delta的特性
Delta值的公式是:選擇權價格變化 / 標的物價格變化。不過通常軟體上都可以查詢的到,只是會有些許誤差,我們的選擇權工具比較精準。
買權的Delta會介於 0 ~ 1 之間,而賣權的Delta會介於 0 ~ -1 之間。你的部位如果是偏多的,那你部位的Delta會是 > 0,例如看多價差、期貨多單。如果你的部位偏空,則是會 < 0,例如看空價差、期貨空單。越往價外履約價的Delta絕對值就越接近 0,反之,越往價內履約價的Delta絕對值則是越接近 1。
Delta中性策略
選擇權由於可以同時做多又做空,這樣的做法也會被稱為Delta中性策略(Delta Neutral),例如跨式勒式策略、兀鷹蝴蝶策略,這些都是Delta中性的策略,你也可以自己用券商軟體實際操作一次買進價平的買權與賣權,你的Delta會很接近 0 (很難完全貼近 0,只能做到接近),賣出價平的買權與賣權也是同樣的道理。
基於這樣的特性,我們可以使用對沖策略,讓方向的風險變成中性,改為賺取時間或是賺取波動的獲利,例如雙賣(賣出跨式、賣出勒式),就是改成賺取時間價值,而不是依靠看漲看跌來獲利。
Delta的運用
最常見的一種運用方式,就是透過Delta的計算來替你的部位做動態避險。一口小台期貨多單的Delta是 1,我若想要替這一口小台多單做避險,那麼我可以考慮買進兩口價平的賣權(-0.5 * 2),如此一來,我整體的部位就會是 1 + (-0.5 * 2) = 0,方向上不偏多也不偏空,先讓我的小台多單避避風頭,等到我判斷危機過去再平倉這兩口賣權。
當然,我也可以選擇只做一口的賣權,甚至也不一定要做在價平,我想做在價外的位置也可以,假設指數下跌跌破我做的這個價外的位置,我的這口賣權的獲利可以抵銷掉我小台多單的虧損。
作為獲利機率看待
Delta還有一個特點是它的絕對值可以作為獲利機率來看待,舉例來說,目前指數20000,而你看到20500這個履約價的買權Delta是 0.2,這代表目前指數有 20% 的機率會漲破20500。
所以假如你賣出一口Delta 0.2 的買權以及一口Delta -0.2 的賣權,你的這組部位會有 100% – 20% – 20% = 60%,意味著你的這組雙賣粗估有 60% 的勝率。
反過來說,如果你是買進一口Delta 0.3 的買權,那麼你能成功獲利的機率可以粗略地當作是 30%。
至於為什麼會有這樣的應用,這跟幾何布朗運動計算價格機率有關聯,而這個計算出來的機率與Delta值相差不遠,所以在應用上會有這樣的做法。








