選擇權價格中隱含的波動率並非對所有履約價一視同仁,而是會隨履約價不同呈現出獨特的曲線形態,俗稱「波動率微笑」或「波動率偏斜」。瞭解這些現象有助於交易者洞察市場情緒、優化定價策略,甚至發現套利機會。本文將分為三個層次深入解析波動率偏斜的概念與應用。
1. 基礎層次:波動率微笑與偏斜的基本概念
波動率微笑與波動率偏斜的定義
「波動率微笑」(Volatility Smile)指同一標的相同到期日下,不同履約價選擇權的隱含波動率 (Implied Volatility, IV) 分佈呈現U形曲線:深度實值 (ITM) 和深度虛值 (OTM) 選擇權的IV高於平值 (ATM) 選擇權。在圖形上,這種對稱的U形曲線看起來就像一個笑容,因此得名「微笑」。相較之下,「波動率偏斜」(Volatility Skew)通常指隱含波動率曲線向一側傾斜的不對稱形狀,也稱「波動率歪斜」或「微笑扭曲 (smirk)」。例如,在某些市場中,我們觀察到OTM選擇權一側的IV明顯高於另一側,曲線呈單邊上揚或下斜,這就是波動率偏斜的現象。
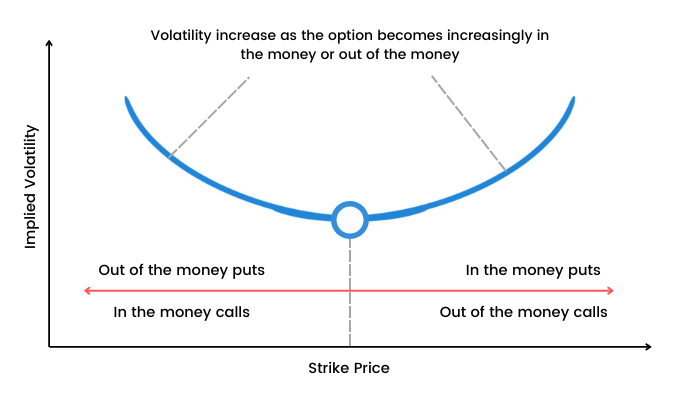
典型的波動率微笑示意圖。橫軸為履約價相對標的現價的比率(虛值程度),縱軸為對應選擇權的隱含波動率。可以看到深度實值與深度虛值選擇權的IV較高,平值附近最低,形成U形曲線。此現象揭示市場認為價格有較大機率發生極端變動(向上或向下),因此兩端的期權價格隱含了更高的預期波動。
不同履約價隱含波動率不同的原因
在理論上的Black-Scholes模型中,假設標的資產波動率固定不變,但現實市場遠非如此。實務中隱含波動率會因履約價不同而改變,其成因與以下因素有關:
- 極端事件機率與報酬分配偏態:歷史經驗表明市場報酬分配具有胖尾特性,極端漲跌發生的可能性高於常態分配預期。1987年「黑色星期一」股災後,交易者開始將大跌的風險反映到選擇權價格中,使深度虛值賣權的IV大幅上升,從而形成了明顯的波動率微笑/偏斜。換言之,市場對左側尾部風險(股價驟跌)的擔憂,會推高遠價外賣權的隱含波動率,以反映潛在劇烈下跌的可能性。
- 避險需求與供需失衡:投資人往往視下跌風險大於上漲潛力,尤其在股市中股票最糟只能跌到零,但上漲理論上無上限。因此投資人更願意付高價買進賣權來避險(對沖下跌),相對地對買權的需求較低。當大量資金湧入價外賣權避險時,這些賣權需求上升、價格被推高,導致其IV明顯高於其他履約價。反之,在某些商品或特殊情況下,投資人可能憂慮標的飆漲(例如商品供給中斷導致價格急升),因而爭相買入價外買權避險上行風險,使得高履約價買權IV高於低履約價,形成另一種方向的偏斜。
- 市場供應特性:在缺乏放空機制或放空成本高的市場中(例如許多個股或新興市場),投資人更傾向透過買入賣權來對沖持股風險,使得反向偏斜(負偏斜)更常見。相反地,在商品等市場,產業避險者(如生產商)經常買入賣權、賣出買權鎖定價格,而投機者追逐看漲期權,導致正向偏斜(高履約價IV偏高)較為常見。
- 事件風險與短期波動:重大事件前後,特定履約價的期權需求會飆升,造成IV曲線局部畸形。例如財報、公投、政策公告等事件若被預期將引發大行情,相關價位的買權或賣權可能出現IV跳升,使波動率曲線在事件前呈現臨時的偏斜或微笑,事件過後又回歸正常。
常見圖形與市場實例
不同市場往往呈現不同形狀的隱含波動率曲線。一般來說,外匯市場常見對稱的波動率微笑,即遠價外的看漲與看跌期權IV皆較高;股票指數等權益市場則多為偏斜(smirk),即OTM賣權IV高於OTM買權,曲線向左上方傾斜(負偏斜);某些大宗商品則可能出現右偏斜(正偏斜),OTM買權IV高於賣權。下圖展示了典型的偏斜形狀:
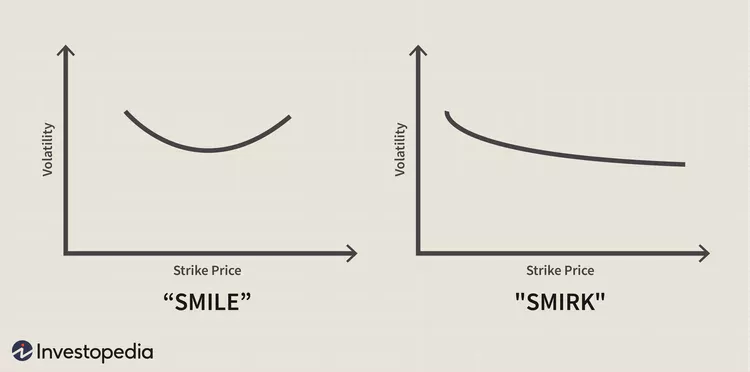
波動率偏斜示意圖(負偏斜)。橫軸為履約價,縱軸為隱含波動率。可見較低履約價(價外賣權)對應更高的IV,隨履約價增加IV逐漸下降。這種形態反映市場對下跌風險的高度重視:投資人支付溢價買入保護性賣權,使得左側尾部隱含波動率被顯著推高。偏斜程度越陡峭,表示市場避險情緒越強烈,對極端下跌的擔憂越大。
實際案例方面,1987年股災後美國S&P500指數選擇權長期呈現明顯的負偏斜,反映投資人持續為「黑天鵝」事件付保險費。另有專門衡量尾部風險情緒的指標,如CBOE的SKEW指數(俗稱「黑天鵝指數」),即透過S&P500價外選擇權的隱含波動率偏斜程度來度量市場認知的尾端風險大小。一般SKEW值越高(例如高於150),表示偏斜陡峭、投資人對極端下跌的擔憂程度極高;相反偏斜趨平時,代表市場認為發生劇烈波動的機率較低。
2. 中階應用層次:市場情緒判讀與策略運用
波動率偏斜反映的市場情緒
尾部風險與避險情緒判斷:波動率偏斜的形狀可作為市場情緒的晴雨表。當偏斜明顯向下傾斜(負偏斜)時,意味價外賣權昂貴,市場透過高付費避險下跌,反映悲觀或恐懼情緒佔上風。例如,某段時期若OTM賣權IV大幅高於歷史平均,表示投資人高度擔心劇烈下跌(左尾事件)的可能性,願意支付高溢價買保險,這常被解讀為看空訊號。相反地,若正偏斜(高履約價買權IV更高)較明顯,則暗示市場預期標的大幅上漲機率增加(或上行風險難以透過現貨做空對沖),對應看多或供給擔憂情緒。此外,波動率微笑(雙尾IV皆高)則通常意味市場對雙向大幅波動都有所顧忌,預期未來可能出現劇烈行情,不確定性很高。交易者可將當前隱含偏斜與歷史水平比較:若偏斜陡峭度遠超常態,通常代表當前市場對尾端風險的定價異常提高,可能預示潛在的異常波動風險。
實務上也有指標化的偏斜指數輔助解讀。例如前述CBOE SKEW指數長期在120左右,若升至150以上往往對應市場高度緊張(投資人搶買深度虛值賣權避險),一些研究和觀察指出SKEW飆高後股市常出現回檔或震盪。不過需注意,偏斜反映的是隱含機率分佈而非確定預測:高偏斜表示市場擔心下跌,但不代表下跌一定會發生,只能說明當下避險情緒高漲。
對買權與賣權定價的影響
波動率偏斜直接影響不同履約價買權與賣權的定價水準。當偏斜存在時,相較一條水平(無偏斜)的IV曲線:
- 買權定價:在典型股指負偏斜情況下,價外買權隱含波動率較低,因需求相對不旺。這意味著OTM買權可能比假設平坦波動率時更便宜。因此,看漲期權的風險中性概率隱含值較低,買方能以較低溢價獲得上漲權利。然而在正偏斜的商品市場,深價外買權因IV偏高而變得昂貴,反映市場對極端上漲的定價提高。
- 賣權定價:在負偏斜市場中,價外賣權因避險買盤踴躍而溢價明顯,即保險費昂貴。這導致遠價外賣權價格遠高於常態模型預測,隱含投資人願意付高成本防範暴跌風險。對賣方而言,賣出這些期權能收到豐厚權利金,但必須意識到隱含的尾部風險。一些資深交易員甚至形容:「賣出價外期權很賺錢,但要知道價外期權跳動劇烈,而平值期權更像遵循常態分布」。因此賣方在負偏斜環境下通常會偏好對沖手中的尾部風險(例如用平值期權或期貨動態避險),以免極端行情發生時遭受巨損。
- 風險溢價與隱含分佈:偏斜的存在意味OTM期權隱含了額外的風險溢價。對應到隱含機率分布,就是左尾(或右尾)較厚:例如股指選擇權的IV偏斜表明隱含分佈相對於對稱分佈具有左偏(負偏度)和較高峰度,即較高的極端下跌機率和更尖峭的中間分佈。Black-Scholes假設被打破:市場用更高的隱含波動率為尾部事件定價,這正是對傳統定價模型的一種修正。
總體而言,波動率偏斜使價內、平值、價外期權的相對價格產生偏差。交易者在定價和構建頭寸時需考慮這種偏差,否則可能低估了尾部風險或錯失利用定價差異獲利的機會。
利用偏斜設計選擇權策略
了解波動率偏斜可幫助交易者優化策略選擇。以下介紹兩類常見策略如何結合偏斜程度來運用:
- 垂直價差 (Vertical Spread):垂直價差指買入和賣出同到期日不同履約價的選擇權組合,包括看漲價差(例如牛市價差、熊市價差)和看跌價差。偏斜影響這類價差的成本與盈虧比:當IV曲線斜率陡峭時,價外期權相對昂貴、價內期權相對便宜。因此一個基本原則是賣出隱含波動率較高的腿,買入隱含波動率較低的腿。例如,在牛市看多情境下,若發現正向偏斜不明顯(高履約買權IV僅略高於ATM),則採取買入看漲價差(Bull Call Spread)可能划算;但如果高履約買權IV飆高(forward skew明顯),反而賣出看跌價差(Bull Put Spread)收取信用價差可能成本更低、勝率更高。同樣地,在看空操作時,若偏斜陡峭,賣出深度價外賣權可以收取較高權利金,而買入稍價內的賣權相對便宜,可構成熊市看跌價差。總之,偏斜程度是決定採用買權價差還是賣權價差的重要考量,因為它直接影響價差的收支平衡點與盈虧比。經驗法則是:偏斜高企時,多利用信用價差收取高溢價;偏斜平坦時,借由價差布局方向性部位成本較低。
- 比率價差 (Ratio Spread):比率價差是指不對稱數量的買賣權組合,例如Backspread(多頭比率價差)是在賣出較少數量近平值期權的同時,買入更多數量更虛值期權,以獲取對尾部變動的曝險。當波動率偏斜失衡時,這類策略可用來捕捉偏斜回歸或表達對尾部風險的看法。例如,2024年底比特幣期權市場出現明顯正偏斜(價外看漲期權IV高於看跌期權約25%),導致看跌期權相對便宜。針對這種IV失衡,交易者設計了比率看跌價差策略:賣出1份ATM看跌期權,同時買入2份價外看跌期權。如此一來,利用偏斜造成的低估,看跌期權IV若日後上升或市場大跌時可獲利,而初始淨支出有限且下行風險有限(因賣出的ATM看跌有兩份更低履約價的看跌期權保護)。這其實是一種反向思考:當市場過度偏好某一端(如狂買看漲期權)導致偏斜畸形時,構建反向比率價差去佈局偏斜可能恢復正常的機會。例如上述比特幣案例中,若未來兩個月看跌期權IV回升或價格下跌,比率價差將同時受益於隱含波動率跳升和方向性利潤。當然,比率價差也承擔風險:若偏斜進一步擴大或標的緩漲橫盤,策略可能小幅虧損。因此交易者須權衡偏斜結構的均值回復傾向,結合自己對市場走勢及波動的預期來運用比率價差。
除了上述策略,風險逆轉 (Risk Reversal)也是和偏斜密切相關的操作:同時賣出一端的期權、買入另一端的期權(例如賣出看跌、買入看漲)相當於押注偏斜走向。若認為當前市場避險情緒過高導致賣權昂貴,可賣出賣權、買入買權以收取偏斜溢價,等待恐慌下降偏斜趨平獲利;反之亦然。然而此類交易風險在於一旦市場真的出現尾部事件,損失可能巨大。因此專業交易員常搭配嚴格風控和動態避險來實施偏斜交易策略。
3. 高階策略層次:希臘值影響、套利與量化模型
波動率偏斜變化對Vega、Gamma的影響
波動率偏斜並非靜止不變;它會隨市場情緒和供需動態而變化。而偏斜的變化(例如陡峭程度增加或減弱)會對選擇權頭寸的風險暴露產生影響,主要體現在Vega和Gamma等敏感度上:
- 對Vega的影響:Vega衡量期權對隱含波動率變動的敏感度。當偏斜變動時,不同履約價期權的隱含波動率將非均勻地改變。例如,偏斜陡峭化通常意味著深虛值賣權IV上升、ATM期權IV相對下降。在這種情況下,空頭持有很多價外賣權的投資者即使總體市場波動率不變,仍可能因尾部隱含波動率上升而遭受損失——因為那些賣權的隱含波動率升高對應價格上漲(Vega為負的損失)。同理,多頭若持有價外賣權,偏斜變陡會帶來額外利潤。交易員必須管理這種偏斜風險,常用的方法是計算組合對不同履約價波動率變動的敏感度(有時稱作契形風險),並透過對衝特定履約價的期權來平衡。如有需要,還可利用Vomma (Volga)這類二階希臘值指標,衡量Vega隨波動率變化的速率,進一步捕捉波動率曲線弧度變化對組合的影響。
- 對Gamma的影響:Gamma衡量期權對標的價格變動的二階敏感度(Delta的變化率)。偏斜本身不直接改變Black-Scholes下計算的個別期權Gamma值,但偏斜暗示了標的資產報酬分佈的非對稱,這對整體頭寸管理的Gamma風險有隱含影響。具體而言,深度價外期權在偏斜環境下“隱含”的未來Gamma可能很大:例如在平靜時期,一份遠價外賣權目前Delta與Gamma幾乎為零,但市場給它很高的IV(反映大跌尾部風險)。一旦標的價格真下跌接近該履約價,該期權將快速進入實值區,Gamma會急劇飆升並帶來巨大的Delta變動。因此,偏斜越大,代表尾部事件發生時Gamma衝擊越劇烈。風險管理上,做空大量價外賣權的交易員必須預防這種「潛伏的Gamma」:一旦市場大跌,這些部位Delta突然暴增,需要火速調整避險部位。從另一角度看,有偏斜時傳統Black-Scholes框架的Delta、Gamma計算會因為忽視波動率隨價位變化而產生偏差。因此許多量化交易員在評估組合風險時,會採用當地波動率模型或跳躍擴散模型來修正Gamma暴露,或者引用Zomma(Gamma對波動率變化的敏感度)來衡量波動率微笑對Gamma的不對稱影響。
在存在波動率偏斜的市場中,僅僅Delta中性、Vega中性的組合並不保證風險中性;仍需關注偏斜變動帶來的非線性風險。高階交易員會同時管理「Vega偏斜風險」與「Gamma偏斜風險」:前者指IV曲線形狀改變對組合價值的影響,後者指標的朝尾部移動時組合Gamma暴露重新配置的風險。
Skew套利與跨市場套利應用
波動率偏斜也為套利交易提供了可能。一些對沖基金和專業做市商會專注於相對價值交易,從偏斜的不合理水平中尋找低風險利潤:
- 偏斜套利:理論上,同一標的同到期日的各履約價期權隱含波動率若存在較大差異,就可能構成套利機會。實務上,由於交易成本和風險因素,純無風險套利幾乎不存在,但交易員可以構建組合來賭IV曲線恢復常態。例如,當偏斜陡峭程度明顯超出歷史區間時,可採取收斂交易:賣出高IV端期權、買入低IV端期權,同時用底層資產對衝Delta,以押注偏斜日後趨平。這類策略等於做空偏斜溢價、等待市場恐慌消退。然而需要注意極端情況下偏斜可能進一步擴大,故風控和資金管理至關重要。此外,跨期限套利也是偏斜相關策略之一:比較不同到期日的偏斜形態(水平/垂直偏斜差異),透過日曆價差或對沖組合獲利。例如某到期日偏斜異常高、而鄰近到期偏斜正常,交易者可考慮做空異常偏斜的到期日、對沖另一到期日,賭其回歸均值。
- 跨市場套利:波動率偏斜還可以在相關資產或市場之間進行比較,從中尋找錯位定價。例如指數與個股之間的偏斜差異:股指期權通常偏斜較陡(因為指數大跌時成分股相關性上升,尾部風險更大),而單一股票期權偏斜可能較平緩。專業套利者會運用離差交易 (Dispersion Trading),同時賣空指數期權(收取高尾部風險溢價)並買入一籃子個股期權(支付較低溢價),以賭市場實現波動低於隱含水平且指數偏斜溢價收斂。類似地,在商品市場,可比較相關商品或不同交易所間期權的偏斜,例如如果布倫特原油與WTI原油期權偏斜程度差異大,或黃金與白銀期權偏斜不同步,可能意味某一市場的尾部風險被高估或低估,提供跨市場套利契機。再如波動率指數 (VIX)與指數期權偏斜之間的相對定價,也能構造交易:VIX高企但SKEW低,或反之,都可能是套利者眼中的異常情形。然而跨市場偏斜套利涉及不同標的,需考慮相關性與基差風險,操作複雜度更高,一般為機構投資者所使用。
值得一提的是,實現偏斜套利通常仰賴高度自動化的交易系統和快速的風險對沖能力。因為偏斜套利利潤通常薄如紙,必須嚴控執行成本並精確管理敞口。對大多數普通交易者而言,偏斜套利更多是理解市場結構的學術意義,而非易於實踐的策略。
波動率曲面與量化建模應用
波動率偏斜概念拓展開來,其實是整個波動率曲面 (Volatility Surface)的一部分。波動率曲面是隱含波動率隨履約價(橫軸)和到期時間(縱軸)變化的三維圖景。它包含了垂直偏斜(同到期不同履約價的IV分佈)以及水平偏斜(不同到期的IV差異,即期限結構)。量化金融領域對波動率曲面的研究與應用極為廣泛:
- 模型校準與選擇權定價:由於Black-Scholes假設恆定波動率與市場不符,交易員和金融工程師透過隱含波動率曲面來校準更複雜的定價模型。常見的方法包括局部波動率模型 (Local Volatility)和隨機波動率模型 (Stochastic Volatility)等。這些模型將波動率視為標的價格和時間的函數,能夠產生符合當前波動率曲面的期權價格。例如SABR、Heston、SVI等模型都能生成帶偏斜和微笑的隱含波動率結構。透過調整模型參數(如波動率均值回復速度、波動率的波動程度等),使模型輸出的期權價格隱含波動率與市場曲面吻合,稱為模型校準。一旦校準成功,模型即可用來定價非活躍交易的履約價、或外推/插值中間缺失點,甚至用于奇異/路徑相依期權的定價,確保複雜衍生品的定價和對沖與市場隱含機率分佈一致。
- 風險管理與情境分析:波動率曲面為風險管理提供了重要依據。透過曲面,可以推演各種市場劇烈波動情境下選擇權組合的變化。例如,風控人員會考慮偏斜突然增大或縮小的情境,評估組合P/L變化,這實際上就是讓隱含波動率曲面發生形變,觀察組合的敏感性。此外,VAR(在險價值)模型若能考慮波動率微笑,將更準確預估極端損失風險。在已知微笑可能降低Vega風險的情況下(因為當標的大幅變動時,ATM位置移動、IV曲線形狀也隨之變化,對沖了部分波動率衝擊),風控人員也可以利用歷史微笑動態特性來調整Greeks。總之,量化團隊會運用歷史資料建構波動率曲面隨市場變動的模型(例如Bergomi提出的微笑動態模型),進一步將其融入組合保護和融資決策中。
- 交易決策支持: 對衍生品量化交易者而言,波動率曲面蘊含大量資訊。例如,透過分析曲面的形狀,可以發現哪些履約價或到期日的期權相對便宜或昂貴,從而指導相對價值交易策略。又例如,一條平滑無套利的波動率曲面應滿足一定數學條件(如各方向二階微分不為負等),若市場報價違反無套利約束(可能由於流動性或供需失衡),就會出現明顯的套利空間。量化交易者會即時監控曲面,尋找凸點或凹陷異常之處下手。同時,波動率曲面的演變也可作為市場預期變化的指標:例如曲面整體上抬(IV升高)通常意味市場恐慌上升,而曲面前端升幅遠大於長端意味短期不確定性劇增等等。綜合這些資訊,量化交易者能制定更精準的交易計畫和資產配置方案。
知識總結與交易決策提升
波動率偏斜及其衍生概念為選擇權交易者提供了一扇洞察市場心理與定價異常的窗口。從基礎層面的定義辨識,到中階層次的情緒判讀與策略設計,再到高階層次的風險管理與模型應用,對偏斜的全面理解都能轉化為實際的決策優化:
- 風險意識提升:懂得觀察波動率偏斜,交易者在市場平靜時也能嗅到潛在風險的蛛絲馬跡。例如,偏斜突然陡峭可能提示大型機構正在積極避險,預示市場對未來波動的擔憂加劇。提早捕捉這種信號有助於調整倉位、控制風險敞口。
- 策略選擇更精準:透彻了解偏斜對定價的影響,交易者在設計策略時能游刃有餘地選擇最佳工具。例如面對看多情境,根據偏斜選擇用買權還是賣權構造牛市價差,以取得更高勝率或更大槓桿;再如隱含偏斜極端時,敢於逆向布局偏斜回復的策略(如比率價差)以博取超額利潤。這些微調都直接提升了交易決策的品質和效率。
- 定價套利把握: 對有能力的交易者而言,熟悉偏斜與波動率曲面意味著能嗅到定價錯誤的機會。不論是跨履約價、跨期限甚至跨市場,只要偏斜程度出現不合理偏離,就可能存在低風險套利窗口。即便不從事專業套利,理解這些也可防止自己在流動性不佳時接受劣價(例如不小心高買了包含巨大溢價的尾部期權)。
總而言之,波動率偏斜概念就如同選擇權世界的地形圖,指引著交易者在定價曲面的高低起伏中前行。善用這些知識,交易者可以更全面地洞察市場預期,打造更穩健的組合並逮住價值錯位的良機。隨著對偏斜理解的加深,我們在選擇權交易決策上的信心和專業度也將隨之提升。








