二項期權定價模型（Binomial Options Pricing Model）是一種用於計算期權價值的模型，而風險中性定價（Risk-Neutral Valuation）是其中的重要原理。這篇文章帶大家理解定價期權的方法。
註：期權（Options），也翻譯為選擇權。
二項期權定價模型概述
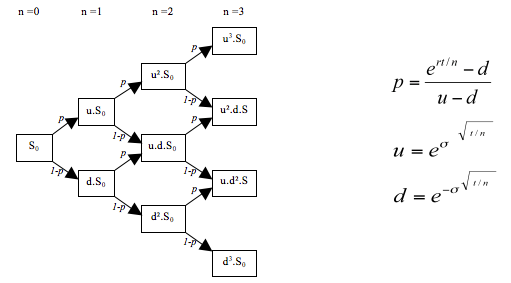
二項期權定價模型是由約翰·考克斯（John Carrington Cox）、斯蒂芬·羅斯（Stephen A. Ross）、馬克·魯賓斯坦（Mark Rubinstein）等人於1979年提出的。該模型假設股價在一段時間內只有兩個可能的方向，上漲或下跌，並且股價的波動率和每個時間段內的概率保持不變。
基於這些假設，二項期權定價模型使用二項樹（binary tree）的結構，將整個期間劃分為多個時間步驟。在每個時間步驟中，根據股價的波動率和概率，模擬出股價的所有可能發展路徑。然後，對於每個路徑上的每個節點，計算相應的期權收益並進行貼現，以獲得期權的價值。對於美式期權，每個節點上的價值取決於行使期權的收益和貼現後的價格，選擇較大的那個值。
二項期權定價模型相對於布萊克-休斯-墨頓模型（Black-Scholes-Merton model）而言，推導過程較為簡單且更具直觀性。它在處理更複雜的期權問題時表現出色，因此成為許多證券交易所的主要定價標準之一。
風險中性定價原理
在討論風險中性定價原理之前，我們需要了解風險厭惡（risk aversion）和風險中性（risk neutral）的概念。風險厭惡表示投資者對風險的承受程度，而風險中性則表示投資者認為確定現金流和不確定現金流的價值相等。
風險中性定價原理指出，在風險中性的假設下，投資者將期望收益按無風險利率進行貼現。換句話說，在風險中性世界中，投資者將對應資產的未來現金流視為確定現金流，並使用無風險利率進行評價。這一原理為期權定價提供了一種方法，將複雜的現實世界問題轉化為簡單的風險中性世界問題。
二項期權定價模型和風險中性定價的應用
二項期權定價模型和風險中性定價在期權定價中有廣泛的應用。二項期權定價模型具有靈活性，適用於不同類型的期權，包括美式期權和百慕大期權。通過構建價格二項樹，我們可以計算出期權在不同情況下的價值。使用這些價值，我們可以確定期權的適當價格，並做出相應的投資決策。
風險中性定價原理使我們能夠在無風險利率框架下對期權進行評價，並確定其合理價格。這種定價方法有助於投資者了解期權價值的形成過程，並根據風險中性的假設做出理性的投資決策。
二項期權定價模型和風險中性定價的結合為我們提供了一種直觀且有效的方法來理解和評價期權。透過對二項樹的建模和風險中性定價的原理，我們能夠根據股價的波動性和概率對期權進行準確的定價。這使得投資者能夠更好地理解期權價值的形成，並在投資決策中作出明智的選擇。
總結起來，二項期權定價模型的思想和風險中性定價原理提供了一個強大而有用的工具，用於評價和理解期權。這些方法的應用使我們能夠更好地解決期權定價的問題，並在投資中做出明智的決策。
延伸閱讀
我們推出了一個使用Ai打造的台股資料line@
方便各位可以快速查詢上市櫃股票的財務數據分析報告
免費工具，歡迎點擊下方圖片加入
推薦閱讀文章
期貨選擇權新手教學影片
有很多人會私訊問我期貨、選擇權的盤後資料應該如何分析，所以我想說乾脆就錄成一部教學影片吧！若是有興趣，可以點擊下方圖片前往填寫你的Email，我會把一部40分鐘的籌碼分析教學影片寄到你的信箱
如果你想要找到一個line群跟大家一起討論期貨選擇權，我也把加入的連結放在信件中了，歡迎你加入我們😊
